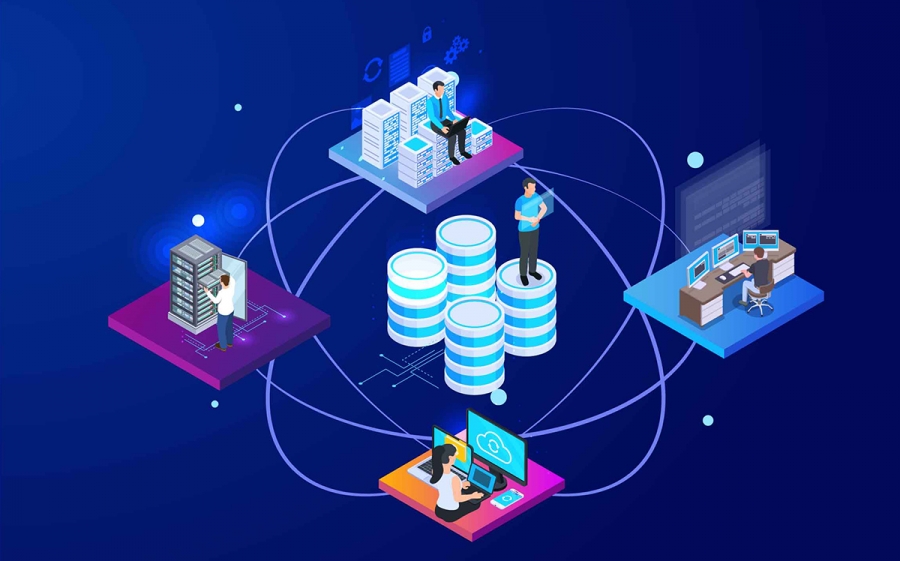
维纳滤波的发展具体是如何的呢?

常用的滤波器是采用电感、电容等分立元件构成,如RC低通滤波器、LC谐振回路等。但对于混在随机信号中的噪声滤波,这些简单的电路就不是最佳滤波器,这是因为信号与噪声均可能具有连续的功率谱。不管滤波有什么样的频率响应,均不可能做到噪声完全滤掉,信号波形的不失真。因此,滤波器研究的一个基本课题就是:如何设计和制造最佳的或最优的滤波器。所谓最佳滤波器是指能够根据某一最佳准则进行滤波的滤波器。
20世纪40年代,维纳奠定了关于最佳滤波器研究的基础。即假定线滤波器的输入为有用信号和噪声之和,两者均为广义稳过程且知它们的二阶统计特,维纳根据最小均方误差准则(滤波器的输出信号与需要信号之差的均方值最小),求得了最佳线滤波器的参数,这种滤波器被称为维纳滤波器。在维纳研究的基础上,人们还根据最大输出信噪比准则、统计检测准则以及其他最佳准则求得的最佳线滤波器。实际上,在一定条件下,这些最佳滤波器与维纳滤波器是等价的。因而,讨论线滤波器时,一般均以维纳滤波器作为参考。维纳滤波是40年代在线滤波理论方面所取得的最重要的成果。
利用稳随机过程的相关特和频谱特对混有噪声的信号进行滤波的方法,1942年美国科学家N.维纳为解决对空射击的控制问题所建立。
维纳滤波的好处有哪些内容?
维纳滤波器的优点是适应面较广,无论稳随机过程是连续的还是离散的,是标量的还是向量的,都可应用。对某些问题,还可求出滤波器传递函数的显式解,并进而采用由简单的物理元件组成的网络构成维纳滤波器。维纳滤波器的缺点是,要求得到半无限时间区间内的全部观察数据的条件很难满足,同时它也不能用于噪声为非稳的随机过程的情况,对于向量情况应用也不方便。因此,维纳滤波在实际问题中应用不多。
实现维纳滤波的要求是:
1.输入过程是广义稳的;
2.输入过程的统计是已知的。根据其他最佳准则的滤波器亦有同样要求;
然而,由于输入过程取决于外界的信号、干扰环境,这种环境的统计特常常是未知的、变化的,因而难以满足上述两个要求。这就促使人们研究自适应滤波器。